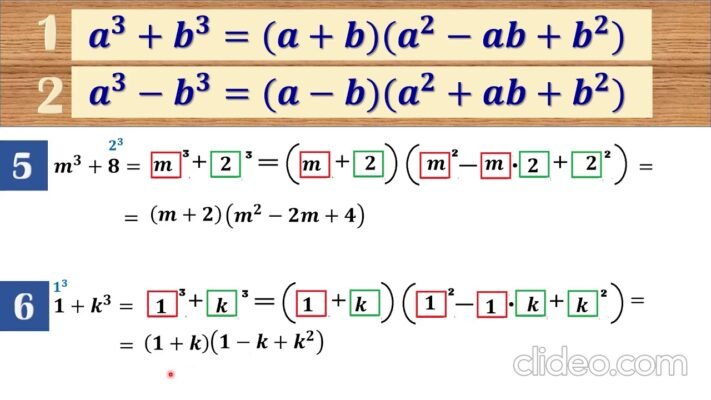
Сума та різниця кубів: алгебраїчні мандри
Сума та різниця кубів… Що манить нас у цій загадковій темі? Це більше ніж просто абстрактні формули — це ключ до гармонії чисел, секретний код, яким можна відкрити таємниці математики. В наші дні ми усвідомлюємо, як важливо розумітися на базових алгебраїчних виразах, адже вони нас оточують. Чому? Тому що ці куби — це інструменти розв’язання складних завдань, які трапляються у житті.
Вступ до світу кубів
Сума кубів — це рівняння виду a³ + b³, а різниця кубів — це a³ – b³. Дивовижно, але ці формули відкривають перед нами багато можливостей. Хоча, ви, мабуть, і не замислюєтесь, скільки ж всього може знадобитися ця штука, поки раптом одного дня… Це схоже на вигадливу гру в шахи, де ваші фігури — це незліченні комбінації з алгебри.
Формули та їх розв’язання
Щоб зануритись у цей світ глибше, давайте глянемо на самі формули. Розпочнемо з простої суми та різниці кубів:
- Сума кубів: a³ + b³ = (a + b)(a² – ab + b²)
- Різниця кубів: a³ – b³ = (a – b)(a² + ab + b²)
На перший погляд, ці формули можуть здатися хаосом. Може здатись, що в цьому і немає сенсу, але… тут є баланс, гармонія. Нехай простим прикладом буде a = 2, b = 3:
- Сума кубів: 2³ + 3³ = 8 + 27 = 35
- Різниця кубів: 2³ – 3³ = 8 – 27 = -19
Це просто магія! Але дивіться далі, як це пов’язується з реальними ситуаціями і задачами.
Застосування у реальному житті
Де ж ми можемо застосувати такі знання? Уявіть собі, що ви інженер, архітектор або навіть розробник ігор. Звичайно, ваш мобільний телефон або така проста річ як кубик Рубіка — все це є частиною рівняння. Кожний день, навіть не думаючи про це, ви зустрічаєтесь з результатами застосування цих формул. Давайте поглянемо на приклади:
| Галузь | Приклад використання |
|---|---|
| Будівництво | Розрахунок об’ємів кубічних споруд |
| Технології | Алгоритми в комп’ютерній графіці |
| Фізика | Моделювання рухів тривимірних тіл |
Спрощення життя? О так. Це дійсно економить час, спресовує зусилля, коли знаєш, як користатися формулами суми та різниці кубів — наче стискати величину в маленький компактний вираз.
Емоційний аспект — чому це важливо?
Але не тільки формули живлять інтерес. За цими рівняннями криється щось більше — поняття рівноваги і переходів. Деякі з нас можуть знайти у цьому своєрідну втіху, бажання зрозуміти, як працює світ. Математика інколи буває такою ж магічною, як літературні твори або музика. Вона вчить нас бачити однакові речі з різних сторін. Іноді всього лише формула може принести більше ніж сухі знання.
Від абстракції до реальних рішень
Скільки разів ми чуємо, що математика — це абстракція? Однак хочеться сказати: вона — самий реальний всесвіт. Ви хочете щось змоделювати? Витратити час на обчислення? Немає проблем! Економіка, логістика, технології – всіх їх важко уявити без цих основоположних знань.
Гра цифрами: приклади
Математика — це не лише обчислення. Вона, як шахи, як ребус – розв’язуємо і розв’язуємо… Можливо, сьогодні ми захочемо заглибитися у багатство цих незвичайних виразів, які нам відкривають неабияке поле для роздумів.
Одного ясного дня, сидячи за столом, ви можете виявити, що всі ці формули з’являються у вашій праці у різних неймовірних ситуаціях. Зрештою, один і той самий куб може обернутись неочікувано важливим для складних систем взаємозв’язку — що, в свою чергу, виразиться у вашій життєвій практиці.
Саме ці невеличкі куби дозволяють нам поглянути на все по-іншому, не зупинятися на банальних обчисленнях. Треба просто трохи подумати, щоб зрозуміти форму і зміст, а математика — тут про баланс і неймовірне відкриття.
Заключні думки
Ви, можливо, вже здатні дивитись на суму та різницю кубів не так, як раніше. Це ж не просто числова гра! Це — карта, що веде до розуміння глибоких законів нашого всесвіту. Це шанс розширити світогляд і збагатити пам’ять чимось більшим, ніж просто алгебраїчними формулами. Світ стає трішки простішим, якщо ми знаємо, як керувати та використовувати свою «кубічну» і не тільки складність. І хто знає, можливо, одного разу ви знайдете себе за розробкою власних формул у цій дивовижній мандрівці…математичною пластиною свого життя.