Різниця Векторів Формула
Поняття різниця векторів формула — це основа, на якій будується багато математичних та фізичних досліджень. Вектори — це не просто стрілки на полях; це об’єкти, які мають напрямок і величину, дозволяючи нам описувати світ у найрізноманітніших аспектах. А різниця векторів, виражена формулою, дозволяє зрозуміти, як змінюються ці об’єкти в просторі.
Що таке вектор?
Вектор — це не просто стрілочка, що простягається від однієї точки до іншої. Це математичний об’єкт, який має дві основні характеристики: величину та напрямок. І хоча багато хто звик вважати векторами лише ті, що існують на плоскій поверхні, насправді вони здатні описувати об’єкти у тривимірному просторі.
- Величина — довжина вектора. Виражається у числовій формі. Наприклад, довжина 5 одиниць чи 12 кілометрів.
- Напрямок — задає ориентацію вектора в просторі. Зазвичай описується кутом або координатами на площині/у просторі.
Диференціація Векторів: Яким Чином? Як?
Дійсно, як рахувати різницю векторів? Що, якщо я скажу, це просто векторний “віднімання”? Завтра настає новий день, а ми вже знаємо, як діють вектори. Давайте заглибимося в цей процес.
Формула для Різниці Векторів
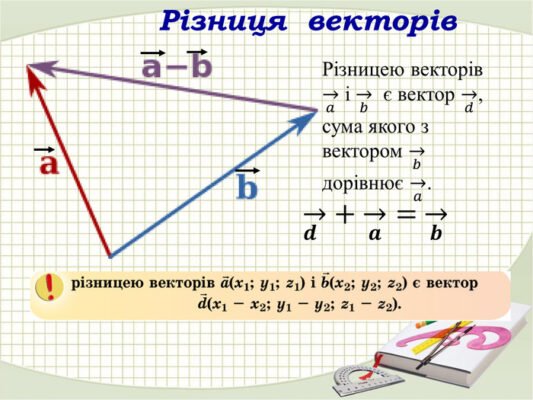
Формула різниці двох векторів виглядає так:
C = A – B
Як це працює? Скажи, що я маю два вектори A (3, 4) та B (1, 2). Тоді різниця буде:
- Різниця по x-осі: 3 – 1 = 2
- Різниця по y-осі: 4 – 2 = 2
Отримаємо новий вектор C (2, 2). Всього лише.
Геометрична Інтерпретація
А тепер уявимо… малюнок: на площині, де видно вектори A і B, які наче тягнуться у різні боки. Різниця векторів формула навчить нас описувати цей процес не математичною мовою, а геометричною — зрозумілою. Як же воно виглядає? Коли ми відкладаємо один вектор від іншого, ми наче зменшуємо довжину першого на величину другого.
Як Це Застосовується?
Побачити вектори можна на нашому улюбленому прикладі — скільки часу треба, щоб велосипедист дістався від пункту А до пункту Б, беручи до уваги швидкість вітру. Відомо, вітряно у місті. На скільки сповільниться шлях? Вектор швидкості — те, що треба.
Точність І Складнощі: Тривимірні Простори
Домалюймо ще вісь z та побачимо: та сама формула, а ось результат — дещо складніший. Вектори можуть “загубитися” у просторі, якщо не правильно вимірювати координати. Тільки додавання осі z дає можливість описати наш об’єкт у повній мірі. Варто пам’ятати:
- Величина змінює все
- Скісні площини — не більше ніж ілюзія
- Тривимірна модель — наша реальність
Практичність Виро___ваного Вищих Знань
Ви думаєте, де ж це все застосувати у житті? Завжди, коли у нас є об’єкт, який змінює своє положення під впливом іншого об’єкту, тут стосується різниця векторів формула. Можливо, ви раніше не помічали, але вона всюди! І навіть, коли ви просто йдете по вулиці — фізика не дозволить вам загубитися у просторі.
| Назва прикладу | Опис |
|---|---|
| Літак | Пілот калібрує напрямок руху враховуючи вектор вітру |
| Плавання | Плавець розраховує траєкторію, враховуючи течію |
| Автомобіль | Водій розраховує шлях враховуючи з’їзд та підйом |
Заключні Думки
Таким чином, поняття різниця векторів формула може здаватися абстрактним і трохи складним на перший погляд, однак воно є невід’ємною частиною нашого розуміння руху і взаємодії об’єктів у просторі. Далі більше — майбутнє вже тут. І важливо, що вже сьогодні ми маємо зрозуміти сутність векторів, їхню реальну роль у світі. Тож, вивчайте, застосовуйте й переймайтесь!