Сума і різниця векторів
Сума і різниця векторів — феномен, який на перший погляд здається суто геометричним, але ж… Цікаво ж розібратися в глибині цього питання. Вектори, ці маленькі стрілки на папері або екрані, здатні вражати уяву своєю простотою та складністю водночас. Їхня сила полягає в можливості представляти фізичні величини, які мають напрямок і величину. І коли ми говоримо про суму та різницю векторів, це вже стосується не лише чисел і символів на карті геометрії, але й того, як вони перетворюють світ навколо нас.
Що таке вектори та їхня природа?
Вектори — це математичні об’єкти. Часто описуються як стрілки в просторі, де їхня довжина представляє величину, а напрямок — вказує, куди ця величина спрямована. Візуалізація векторів може бути суперською для розуміння фізичних процесів. Чому? Бо вони дозволяють легко уявити сили, швидкості, напрямки руху. Тут немає місця простій арифметиці, зате є “векторна” магія, де складання — це ніби нове рівняння на площині або навіть у просторі.
Сума векторів
Давайте почнемо з простішого — операція складання векторів. Уявимо, у нас є два вектори: a і b. Щоб знайти їхню суму, вирівнюємо початок b з кінцем a. Лінія, яка з’єднує початок a з кінцем b, є їхньою сумою.
Алгоритм складання векторів
- Розташуйте початок другого вектора у кінці першого.
- Проведіть стрілку від початку першого до кінця другого — це сума.
- Результуючий вектор буде мати нову величину і напрямок.
І, здається, нічого складного, але… Які чудеса можуть породити ці невеличкі маніпуляції у відображенні реальних явищ світу!
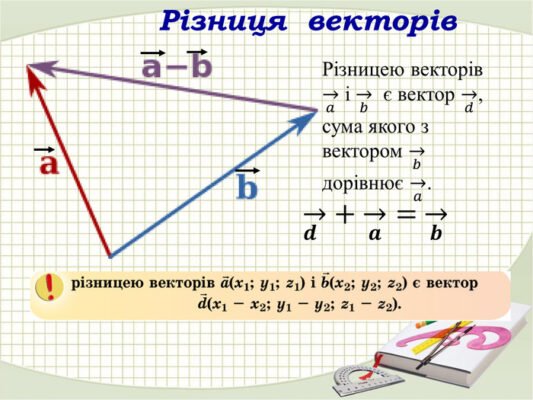
Різниця векторів
Тепер про різницю. Знову беремо два вектори, a і b. Але тепер запитується: як би виглядав вектор, якщо b “відняти” від a? Теоретично, треба взяти інверсію b (змінити його напрямок на протилежний) і вже цю протилежність — до суми з a.
Процес обчислення різниці
- Зворотний вектор b позначається як –b.
- Виконуємо суму a + (-b).
- Так отримуємо вектор різниці a – b.
І от вже бачимо, що різниця векторів — це теж своєрідна “операція з додаванням”, але з хитрістю напрямку.
Практичні застосування: де це важливо?
Навіть якщо ти далеко від фізики, вектори оточують нас постійно. Уявімо собі площину чи простір, вектори літають і переміщаються так, як тільки їм до вподоби. Їхня динаміка може відображати рух автомобілів, літаючих об’єктів, силу вітру — словом, різноманітні природні явища.
Приклади використання:
| Сфера | Застосування |
|---|---|
| Фізика | Опис сил, швидкостей, прискорень |
| Інформатика | 3D моделювання, графіка |
| Інженерія | Проектування структур, статика |
Додамо ще свої 5 копійок. Допоможіть вашій уяві, нехай вона бігає вільно… переставте вектори в голову і знайомтеся з новими способами мислення.
Вектори в житті. Незвичне й цікаве
І ось ще одна штука, про яку мало хто задумується. Вектори — це не просто математичні формули. Це радше мова, інструмент, завдяки якому ми можемо описати навколишній світ. Вони, так би мовити, живуть своїм життям, як автомобілі на дорозі, літаки в небі, чи навіть класи в школі.
Відчуваєте, як атмосферно вектори можуть змінити сприйняття світу? Допомагають бачити напрямок, відчувати силу та розуміти механіку. Дивовижно, чи не так? Вектори ніби маленькі маги на площині і в просторі, що з’єднують світ числа і реальності.
Наостанок: сума і різниця як один із аспектів світосприйняття
Із цікавістю погляньте за межі підручників. Сума і різниця векторів — це більше, ніж просто технічний навик. Це свого роду мистецтво. Наука, яка поєднує в собі красу математики з практичністю реального світу. Придивляйтеся до цих непомітних ліній, що творять силу в кожному русі, в кожній силі, кожній швидкості. І нехай вони стануть вашими новими старими друзями.